五大常见算法策略之——动态规划策略（Dynamic Programming）

  Dynamic Programming是五大常用算法策略之一，简称DP，译作中文是“动态规划”，可就是这个听起来高大上的翻译坑苦了无数人，因为看完这个算法你可能会觉得和动态规划根本没太大关系，它对“动态”和“规划”都没有太深的体现。
  举个最简单的例子去先浅显的理解它，有个大概的雏形，找一个数组中的最大元素，如果只有一个元素，那就是它，再往数组里面加元素，递推关系就是，当你知道当前最大的元素，只需要拿当前最大元素和新加入的进行比较，较大的就是数组中最大的，这就是典型的DP策略，将小问题的解保存起来，解决大问题的时候就可以直接使用。
  刚刚说的如果还是感觉有点迷糊，不用慌，下面几个简单的小栗子让你明白这句话的意思。

Fibonacci再讨论

  第一个数是1，第二个数也是1，从第三个数开始，后面每个数都等于前两个数之和。要求：输入一个n，输出第n个斐波那契数。
  还是我们上节讨论递归与分治策略时候举的第一个例子——Fibonacci数列问题，它实在太经典了，所以将其反复拿出来说。
  我们如果深入分析一下上节说过的递归方法解决Fibonacci数列，就会发现出现了很多重复运算，比如你在计算f(5)的时候，你要计算f(4)和f(3),计算f(4)又要计算(3)和f(2),计算f(3)，又要计算f(2)和f(1),看下面这个图

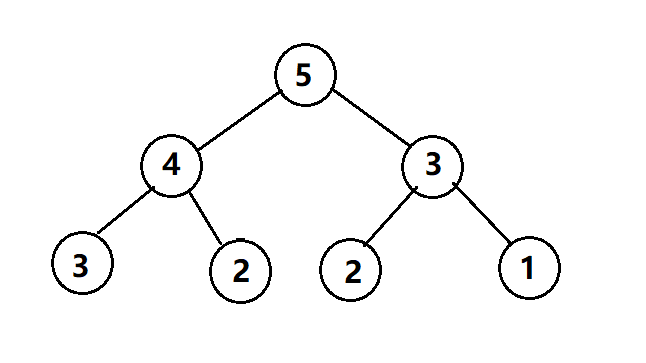
对f(3)和f(2)进行了重复运算，这还是因为5比较小，如果要计算f(100),那你可能要等到天荒地老它还没执行完（手动滑稽），感兴趣的朋友可以试试，反正我已经试过了。

public static int fibonacci(int n){//递归解法 if(n == 1) return 1; else if(n == 2) return 1; else return fibonacci(n - 1) + fibonacci(n - 2); }

上面就是递归的解法，代码看着很简单易懂，但是算法复杂度已经达到了O(2^n),指数级别的复杂度，再加上如果n较大会造成更大的栈内存开销，所以非常低效。
我们再来说说DP策略解决这个问题
我们知道导致这个算法低效的根本原因就是递归栈内存开销大，对越小的数要重复计算的次数越多，那既然我们已经将较小的数，诸如f(2),f(3)...这些计算过了，为什么还要重复计算呢，这时就用到了DP策略，将计算过的f(n)保存起来。我们看看代码：

/** * 对斐波那契数列求法的优化：如果单纯使用递归，那重复计算的次数就太多了，为此，我们对其做一些优化 * 假设最多计算到第100个斐波那契数 * 用arr这个数组来保存已经计算过的Fibonacci数，以确保不会重复计算某些数 */ private static int arr[] = new int[100]; public static int Fibonacci(int n){ if(n <= 2){ return 1; }else{ if(arr[n] != 0) //判断是否计算过这个f(n) return arr[n]; else{ arr[n] = Fibonacci(n-1)+Fibonacci(n-2); return arr[n]; } } }

arr数组初始化为0，arr[i]就表示f(i),每次先判断arr[i]是否为0，如果为0则表示未计算过，则递归计算，如果不为0，则表示已经计算过，那就直接返回。
 
这样的好处避免了很大程度上重复的计算，但是对栈内存的开销虽然有减小但还不是很显著，因为只要有递归，栈内存就免不了有较大开销。所以针对Fibonacci数列我们还有一个递推的方式来计算，其实这也符合DP策略的思想，都是将计算过的值保存起来。

//甚至可以使用递推来求解Fibonacci数列 public static int fibonacci(int n){ if(n <= 2) return 1; int f1 = 1, f2 = 1, sum = 0; for(int i = 3; i <= n; i++){ sum = f1+f2; f1 = f2; f2 = sum; } return sum; } 求解路径个数

一个机器人每次只能向右或者下走一步，问它试图到达右下角“Finish”，共有多少条不同的路径？(7*3的网格)

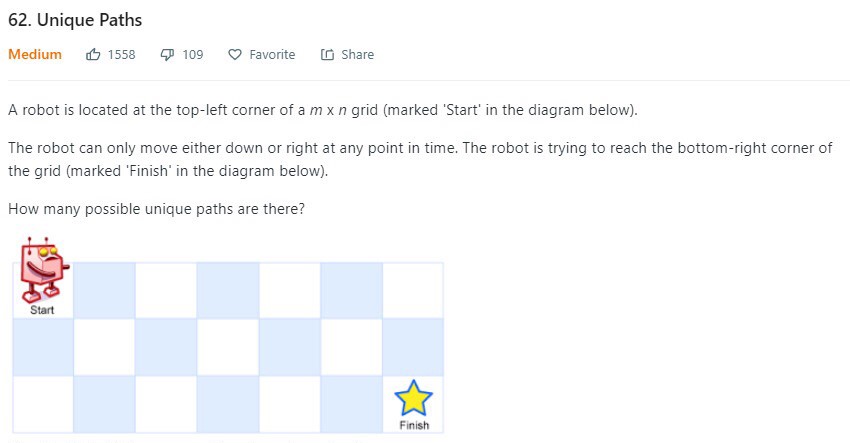
DP策略类的题最重要是要找状态转移方程，恰恰也是最难的一步。

1、我们通过这个图可以看出其实要到达(i,j)也就两种情况，一种是从(i,j-1)向右走一步到达，另一种是从(i-1,j)向下走一步到达，所以将这两种情况的路径数相加就是到(i,j)的所有路径数。

由此列出状态转移方程： f(i,j)=f(i-1,j)+f(i,j-1)

2、根据DP的思路，将已经计算过的存储起来并用于后面复用其结果，这里我们考虑用二维数组来存储f(i,j)。

3、问题规模从小到大计算，大规模的问题复用小规模问题的解进行计算。
代码实现

/** * 此题是求解路径个数，让你从(1,1)走到某个特定的位置，求一共有多少种走法 * @param i * @param j * @return */ public static int Count_Path(int i, int j){ int result[][] = new int[i][j]; for (int k = 0; k < i; k++) { //将二维数组初始化为1 Arrays.fill(result[k],1); } for (int k = 1; k < i; k++) { for (int l = 1; l < j; l++){ result[k][l] = result[k-1][l]+result[k][l-1]; } } return result[i-1][j-1]; } 小青蛙跳台阶再讨论